딥러닝 기반 자연어처리 기초 - RNN, etc

Sequnce to Sequnce

• Sequnce to sequence 
  입력된 시퀀스 (문장)을 다른 시퀀스로 변환하는 모델, 인코더 RNN과 디코더 RNN로 구성
  자연어 입력 - 인코더 / 자연어 출력 - 디코더
  

  

  출처 : https://lilianweng.github.io/posts/2018-06-24-attention/

  
  
  • 인코더 (Encoder)
    입력 시퀀스를 받아들여 고정된 길이의 벡터로 변환. 이 벡터는 입력 시퀀스의 정보를 압축적으로 담고 있음.
    이 벡터를 문맥 벡터 (Context Vector)라고 부름.
    
    
  • 디코더 (Decoder)
    문맥 벡터를 받아들여 출력 시퀀스를 생성
    디코더는 문맥 벡터와 이전에 생성한 출력을 기반으로 다음 출력을 생성
    
    
    • auto regressive & auto encoding
      보통 auto regressive 방식으로 출력됨.
      auto regressive의 반대말은 auto encoding.
      간단한게 auto encoding은 모델이 입력된 것을 이해하는 방식이고, auto regressive는 학습된 모델이 숫자들을 출력하는 방식을 의미. 

RNN 이해하기

• Recurrent Neural Networks (RNNs)
  시계열을 다루는데 효과적인 데이터 
  
  언어는 순서대로 생성됨. 시계열적인 특성이 있음. 
  
  반면 이미지는 순차적인 정보가 없음. 그렇기 때문에 RNN이 적합하지 않음. 
  CNN과 같은 parallel하게 처리하는 모델이 적합.
  

  

  출처 : https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks

  
  $a^{<t-1>} , a^{<t>}$: 이전 시간 단계(t-1)와 현재 시간 단계(t)에서의 hidden state를 나타냄. 이는 RNN의 “메모리" 역할을 하며, 이전 시간 단계의 정보를 현재 시간 단계로 전달함
  $W_{aa}, W_{ar}, W_{ya}$: 각각 이전 hidden state, 현재 입력, 현재 hidden state에 대한 가중치를 나타냄.
  $x^{<t>}$: 현재 시간 단계에서의 입력을 나타냄
  $g_{1},g_{2}$ : 활성화 함수, g_1은 보통 tanh와 같은 비선형 함수를 사용, g_2는 출력의 형태에 따라 다르게 선택
  
  $a^{<t>} = g_{1}(W_{aa}a^{<t-1>} + W_{ax}x^{<t>} + b_{a})$
  
  $y^{<t>} = g_{2}(W_{ya}a^{<t>} + b_{y})$
  
  이전 hidden state $a^{<t-1>}$ 을 받고 현재 상태 입력인 $x^{<t>}$ 를 입력한다.
  그로 인해서 나오는 hidden state가 $a^{t}$ 이다.
  마지막으로 $y^{<t>}$ 가 출력됨.
  
  
  • 손실함수 (Loss function)  
    
    $L\left( \widehat{y},y\right)$ $= \sum ^{T_{y}}_{t=1}L\left( \widehat{y}^{<t>},y^{<t>}\right)$ 
    
    
  • 시간 순서 역전파 (Backpropagation through time)
    $\dfrac{\partial ^{ (T) }}{\partial W} = \sum_{t=1}^{T}\frac{\partial L^{(T)}}{\partial W} 
    \left.\begin{matrix}
     \\
     \\
    \end{matrix}\right|_{(t)}$
    
    
  • RNN 종류
    

    

    출처 : https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks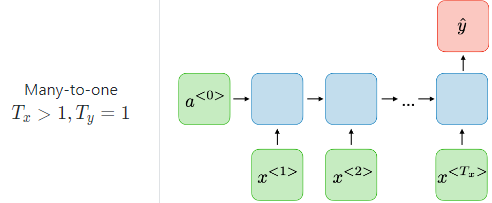

    

    출처 :&nbsp;https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks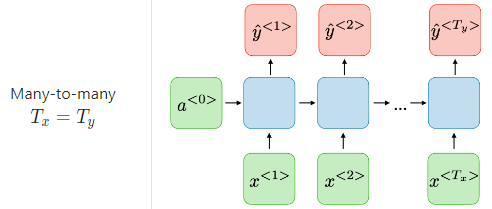

    
    

    

    출처 : https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks

    
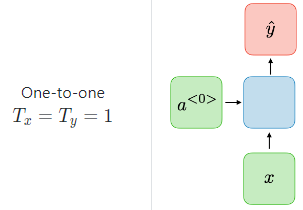
    one to one : Traditional neural network. 이미지 분류
    one to many : 1개의 입력으로 많은 시퀀스를 출력. 이미지 captioning 
    many to one : 문장 여러개고 1개 출력. 감정 분석
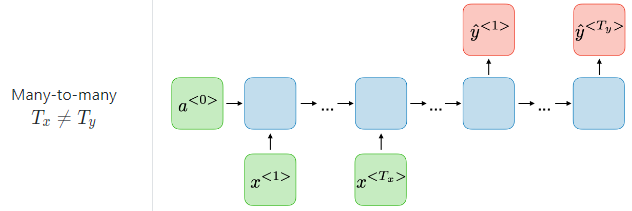
    many to many : 기계 번역, 형태소 분석 등등.
    
    
  • RNN의 장점
    • 모든 길이의 시퀀스를 입력으로 처리 가능
    • 시간에 따라 가중치를 공유하여, 입력 시퀀스가 길어져도 모델 크기가 증가하지 않음
    • 과거 정보를 고려하여 다음 시간의 출력을 계산함
    
    
  • RNN의 단점
    • 매번 시간에 따라 출력을 계산하므로, 병렬 처리가 불가능하여 계산 속도가 느림
    • 입력 혹은 출력 시퀀스가 길어지면 오래전 정보를 반영하기 어려움 (Long-term dependency)
    • 현재 상태에 대한 미래 입력을 고려할 수 없음
    
    

LSTM & GRU 이해하기

• Gradient vanishing / exploding
  기존 RNN의 역전파 과정에서 그래디언트가 너무 작아져서(gradient vanishing) 가중치 업데이트가 잘 안 되거나, 그래디언트가 너무 커져서(gradient exploding) 가중치 값이 엄청나게 커지는 문제가 발생
  • 이로 인해 모델이 불안정해지고, 시퀀스 데이터의 장기 의존성을 제대로 학습하지 못하게 됨
  
  
• Long Short-Term Memory (LSTM)
  RNN에서 발생하는 Long-term dependency problem 완화 방법으로 LSTM은 cell state와 gate라는 메커니즘을 도입
  • 필요한 정보만을 선택적으로 업데이트하거나 삭제하는 방법을 도입 (정보를 잘 기억하고 활용)
  
  
  • $\sigma$
    sigmoid 활성화 함수
    • 출력 값의 범위를 [0, 1]로 제한하여, 게이트에서 어떤 정보를 통과시킬지 결정하는 데 사용됨
    
    
  • $\widetilde{C_{t}}$ 
    현재 시간 단계에서의 cell state 후보
    • 현재 입력과 이전 hidden state에 기반하여 계산됨
    
    
  • $C_{t}$
    현재 시간 단계에서의 cell state
    • forget gate가 결정한 대로 이전 cell state의 일부를 잊고, input gate가 결정한 대로 새로운 정보를 추가하여 업데이트됨
    
    
  • $f_{t}, i_{t}, o_{t}$
    forget gate, input gate, output gate
    • 이전 cell state의 어느 부분을 잊을지, 새로운 정보를 얼마나 추가할지, 어느 부분을 hidden state로 출력할지 결정
    
    
  • $ f_{t} = \sigma(W_{f} [h_{t-1},x_{t}] + b_{f}) $
    
    $ i_{t} = \sigma(W_{i}[h_{t-1},x_{t}] + b_{i})$ 
    
    $ \widetilde{C_{t}} = tanh(W_{C}[ht-1,x_{t}] + b_{C})$
    
    $ C_{t} = f_{t} \ast C_{t-1} + i_{t} \ast \widetilde{C_{t}}$
    
    $ o_{t} = \sigma(W_{o}[h_{t-1},x_{t}]+b_{o})$
    
    $h_{t} = o_{t} \ast tanh(C_{t})$
    
    
  • Forget gate
    $f_{t} = \sigma (W_{f}[h_{t-1},x_{t}] +b_{f})$
    
    
    • forget gate layer로, 이전 cell state의 어느 정보를 버릴지 결정 $W_{f}$와 $b_{f}$ 는 학습 가능한 가중치와 편향
      
      
    • 시그모이드 함수 sigmoid는 출력을 0과 1 사이로 제한하여 어떤 요소를 완전히 잊어버릴지 (0) 또는 완전히 기억할지 (1) 결정
      
      
  • Input gate
    $i_{t} = \sigma(W_{i}[h_{t-1},x_{t}] + b_{i})$
    
    
    • input gate layer로, 어떤 새로운 정보를 cell state에 저장할지 결정
      
      $ \widetilde{C_{t}} = tanh(W_{C}[ht-1,x-{t}] + b_{C}) $
      
      
    • 새로운 후보 cell state를 생성. 이후에 후보 cell state 정보 중 일부가 cell state에 저장 
      
      
  • Cell state